The simplest goal of general nonlinear optimization is to find a local minimum of a differentiable function. The majority of general nonlinear optimization methods are based on relaxation, i.e. generating decrease sequence $\{ f(x_k) \}_{k = 0}^\infty$, such that
$$
f(x_{k+1}) \leq f(x_k), ~ k = 0, 1, \cdots.
$$
To implement the idea of relaxation, we employ another fundamental principle, approximation. Usually, we apply local approximation based on derivatives of nonlinear functions. Local methods are discussed in general setting without convexity.
Optimality Conditions
- First order necessary condition (Fermat’s theorem)
- Second order necessary condition
- Second order sufficient condition
Gradient Method
For unconstrained differentiable problems, it can be verified that the antigradient is a locally steepest descent direction, thus gradient method makes move in the antigradient direction.

The step size $h_k$ can be chosen
- as constant or decrease over iteration (mainly in convex optimization)
- by optimize a one dimensional problem (completely theoretical)
$ h_k = \arg \min_{h \geq 0} f(x_k - hf’(x_k))$ - by Goldstein-Armijo rule (commonly used in practical algorithms). Find $x_{k+1} = x_k - hf’(x_k)$, such that
$ \alpha \langle f’(x_k), x_k - x_{k+1} \rangle \leq f(x_k) - f(x_{k+1}) $,
$ \beta \langle f’(x_k), x_k - x_{k+1} \rangle \geq f(x_k) - f(x_{k+1}) $
Denote $\phi(h) = f(x - hf’(x)), ~ h \geq 0$, then the step-size acceptable belong to that part of the graph of $\phi$ that is located between two linear functions:
$ \phi_1(h) = f(x) - \alpha h \| f’(x) \|^2, \quad \phi_2(h) = f(x) - \beta h \| f’(x) \|^2 $
If $\phi(h)$ is bounded below, there exists acceptable step-size.
Convergence Analysis
General Lipschitz continuous objective
For unconstrained problem with $f(x) \in C_L^{1, 1}(\mathbb{R}^n)$ and bounded below, we have
$$
f(x_k) - f(x_{k+1}) \leq \frac{\omega}{L}|f’(x_k)|^2
$$
for some positive constant $\omega$. That leads to $O(\frac{1}{\sqrt(N)})$ convergence rate of $ g_N^* = \min_{0 \leq k \leq N} \| f’(x_k) \| $, which comes from the following result,
$$
g_N^* \leq \frac{1}{\sqrt{N+1}} \left[ \frac{1}{\omega} L(f(x_0) - f^*)\right]^{1/2},
$$
where $f^*$ is the optimal value.
However, we cannot say anything about the rate of convergence of sequences $ \{ f(x_k)\}$ and $\{ x_k\}$. An counterexample, is the following function of two variables:
$$
f(x) = \frac{1}{2} x_1^2 + \frac{1}{4} x_2^4 - \frac{1}{2}x_2^2
$$
If we start gradient descent from $x_0 = (1, 0)$, we will only get a stationary point $x_1^* = (0, 0)$, since $\frac{\partial f}{\partial x_1}$is always zero.
Linear convergence
If the objective satisfies the following assumptions:
- $f \in C_M^{2, 2}(\mathbb{R}^n)$
- there exists a local minimum at which the Hessian is positive definite
- we know some bounds $0 < l \leq L < \infty$ for the Hessian at $x^*$
$ l I_n \preceq f’’(x^*) \preceq LI_n $ - the starting point $x_0$ is close enough to $x^*$, i.e,
$r_0 = \| x_0 - x^* \| < \bar{r} = \frac{2l}{M}$
then the gradient descent method with step size $h_k = \frac{2}{L+l}$ leads to a linear convergence rate,
$$
\| x_k - x^* \| \leq \frac{\bar{r} r_0}{\bar{r}-r_0} \left( 1 - \frac{2l}{L+3l} \right)^k
$$
Newton Method
The Newton method for optimization problems generates points with the following update rule,
$$
x_{k+1} = x_k - [f’’(x_k)]^{-1} f’(x_k).
$$
It can be obtained by
- Minimizing the quadratic approximation of the objective, computed w.r.t. point $x_k$, $\phi(x) = f(x_k) + \langle f’(x_k), x - x_k \rangle + \frac{1}{2} \langle f’’(x_k)(x- x_k), x - x_k\rangle$
- Finding the roots of the nonlinear system $f’(x) = 0$ via Newton method.
Newton method converges very fast. Actually, if the objective satisfies the following conditions
- $f \in C_M^{2, 2}(\mathbb{R}^n)$
- There exists a local minimum with positive definite Hessian: $f’’(x^*) \succeq lI_n, ~ l > 0$
- The starting point $x_0$ is close enough to $x^*$, i.e., $\|x_0 - x^* \| < \bar{r} = \frac{2l}{3M}$
the Newton method converges quadratically:
$$
\|x_{k+1} - x^* \| \leq \frac{M \|x_k - x^* \|^2}{2 (l-M\|x_k - x^* \|)}
$$
Surprisingly, the region of quadratic convergence of the Newton method is almost the same as the region of linear convergence of the gradient method. Overall, it is recommended to use gradient method at the initial stage of the minimization process to get close to a local minimum, and perform the final job by Newton method.
Quasi-Newton Methods
Fix some $\bar{x} \in \mathbb{R}^n$, the gradient method can be obtained by considering the following approximation,
$$
\phi_1(x) = f(\bar{x}) + \langle f’(\bar{x}), x - \bar{x} \rangle + \frac{1}{2h} \|x - \bar{x} \|^2,
$$
which is a $global upper$ approximation, if $h \in (0, \frac{1}{L}]$. And the Newton method is formulated from the quadratic approximation,
$$
\phi_2(x) = f(\bar{x}) + \langle f’(\bar{x}), x - \bar{x} \rangle + \frac{1}{2} \langle f’’(\bar{x})(x - \bar{x}), x - \bar{x} \rangle,
$$
this motivates us to use approximation better than $\phi_1(x)$ while less expensive than $\phi_2(x)$:
$$
\phi_G(x) = f(\bar{x}) + \langle f’(\bar{x}), x - \bar{x} \rangle + \frac{1}{2} \langle G(x - \bar{x}), x - \bar{x} \rangle,
$$
which leads to quasi-Newton methods (also variable metric methods). To be specific, these methods form a sequence of matrices $ \{ G_k \}: ; G_k \rightarrow f’’(x^*)$
(or $\{ H_k \}: ; H_k \rightarrow [f’’(x_k)]^{-1}$), and update the solution with
$$
x_{k+1} = x_k - G_k^{-1} f’(x_k)
$$
(or $x_{k+1} = x_k - H_k f’(x_k)$ ). Only the gradients are involved in the process of generating sequence $\{ G_k \}$ or $\{ H_k \}$.

Justified by the property of quadratic funcion $f(x) = \alpha + \langle a, x \rangle + \frac{1}{2} \langle Ax, x \rangle$,
$$
f’(x) - f’(y) = A(x-y), \ \forall x, y,
$$
the quasi-Newton rule is proposed:
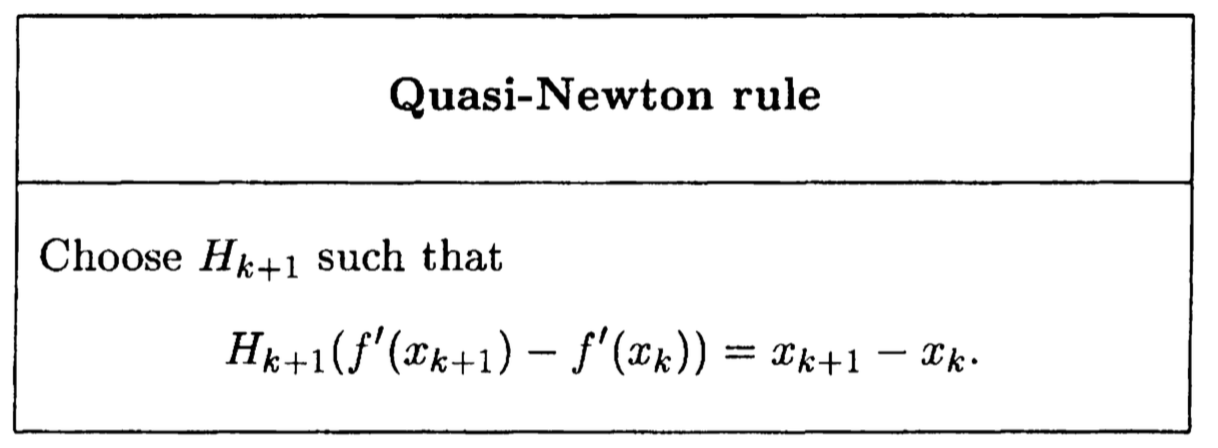
There are many ways to satisfy the rule, which lead to various quasi-Newton methods, such as BFGS, DFP.
Convergence Rate
- In a neighbourhood of strict minimum, quasi-Newton methods have a superlinear rate of convergence: for any $x_0$ there exists a number $N$ such that for all $k \geq N$, we have $\| x_{k+1} - x^* \| \leq \text{const} \cdot \| x_k - x^* \| \cdot \| x_{k-n} - x^* \| $;
- For global convergence, these methods are not better than the gradient method (at least from the theoretical point of view).
Conjugate gradient method
The conjugate gradients methods are initially proposed for minimizing a quadratic function,
$$
\min_{x \in \mathcal{R}^n} f(x) = \min_{x \in \mathcal{R}^n} \alpha + \langle a, x \rangle + \frac{1}{2} \langle Ax, x \rangle,
$$
with $A = A^T \succ 0$. It is obvious that the problem statisfies
- the solution of this problem is $x^* = -A^{-1} a$ and $f^* = \alpha - \frac{1}{2} \langle Ax^*, x^* \rangle $
- the gradient $f’(x) = A(x-x^*)$
The conjugate gradients consider the Krylov subspaces,
$$
\mathcal{L}_k = \text{Lin}\{A(x_0 - x^*), \ldots, A^k(x_0 -x^*)\}, \ k \geq 1,
$$
and theoretically genrate the sequence of points with
$$
x_k = \arg \min \left\{ f(x) , | , x \in x_0 + \mathcal{L}_k \right\}, \ k \geq 1.
$$
This definition is only used for theoretical analysis. For quadratic objective, we have
- $\mathcal{L}_k = \text{Lin }\{f’(x_0), \ldots, f’(x_{k-1})\} = \text{Lin }\{ \delta_0, \ldots, \delta_{k-1} \}$,where $\delta_i = x_{i+1} - x_i$
- for any $k, i \geq 0$, we have $\langle f’(x_k), f’(x_i) \rangle = 0$, if $k \neq i$
- for any $k, i \geq 0$, we have $\langle A\delta_k, \delta_i \rangle = 0$
The second property indicates that we have the solution after $n$ steps, since the number of orthogonal directions in $\mathcal{R}^n$ cannot exceed $n$. The last property explains the name of the method.
The general scheme of conjugate gradients (for minimizing a nonlinear function) :

There are different formulas for coefficient $\beta_k$, all of them lead to the same result for quadratic functions. In general nonlinear case, they generate different sequences.
Convergence Rate
- Restarting: the conjugate gradients terminate in $n$ iterations (or less), for quadratic objectives. However, for general nonlinear case, the conjugate directions lose any interpretation after $n$ iterations. Thus, in all practical schemes, at some moment we sets $\beta_k = 0$ (usually after every $n$ iterations).
- In a neighborhood of a strict minimum, the conjugate gradients schemes have a local $n$-step quadratic convergence: $\|x_{n+1} - x^* \| \leq \text{const} \cdot \|x_0 - x^* \|^2$
- When it comes to global convergence, the conjugate gradients are not better than the gradient method.