上个学期修了计算理论课程,但结果没有去上过几次课,最后勉强没有挂科。但实际上,计算理论是CS之所以能成为科学的重要基础,也是CS中非常有趣的部分。因此选了Coursera的Automata课程,由Stanford的Jeff Ullman教授讲课。教授自然是大神,传说中的龙书(《编译原理》)的作者,当然半路出家的我并没有拜读过,不过封面真是赞啊。
What’s in this course
- Regular languages and their descriptors
- Finite Automata, nondeterministic finite automata, regular expressions
- Algorithms to decide questions about regular languages, e.g., is it empty?
- Closure properties of regular languages
- Context-free languages and their descriptors
- Context-free grammars, pushdown automata
- Decisions and closure properties
- Recursive and recursively enumerable languages
- Turing machines, deciability of problems
- The limit of what can be computed
- Intractable problems
- Problems that (appear to) require exponential time
- NP-completeness and beyond
PS: Ullman教授提到了这样的事实: A survey of Stanford grads 5 years out asked which of their courses did they use in their job.
- Basics like intro-programming took the top spots, of course.
- But among optional courses, CS154 (Automata and Complexity Theory) stood remarkably high.
Week 1 Snippets – Introduction to Finite Automata
Introduction
What is a Finite Automaton
- A formal system
- Remembers only a finite amount of information
- Information represented by its state
- State changes in response to input
- Rules that tell how the state changes in response to inputs are called transitions
An Example
A Tennis consists of 3-5 sets, each of which contains 6 or more games. To score a game, one player serves throughout. To win, you must score at least 4 points. Meanwhile, you must win by at least 2 points.
Suppose the inputs are s = “server wins points” and o = “opponent wins points”. Then all states and transitions can be represented as follow graph.
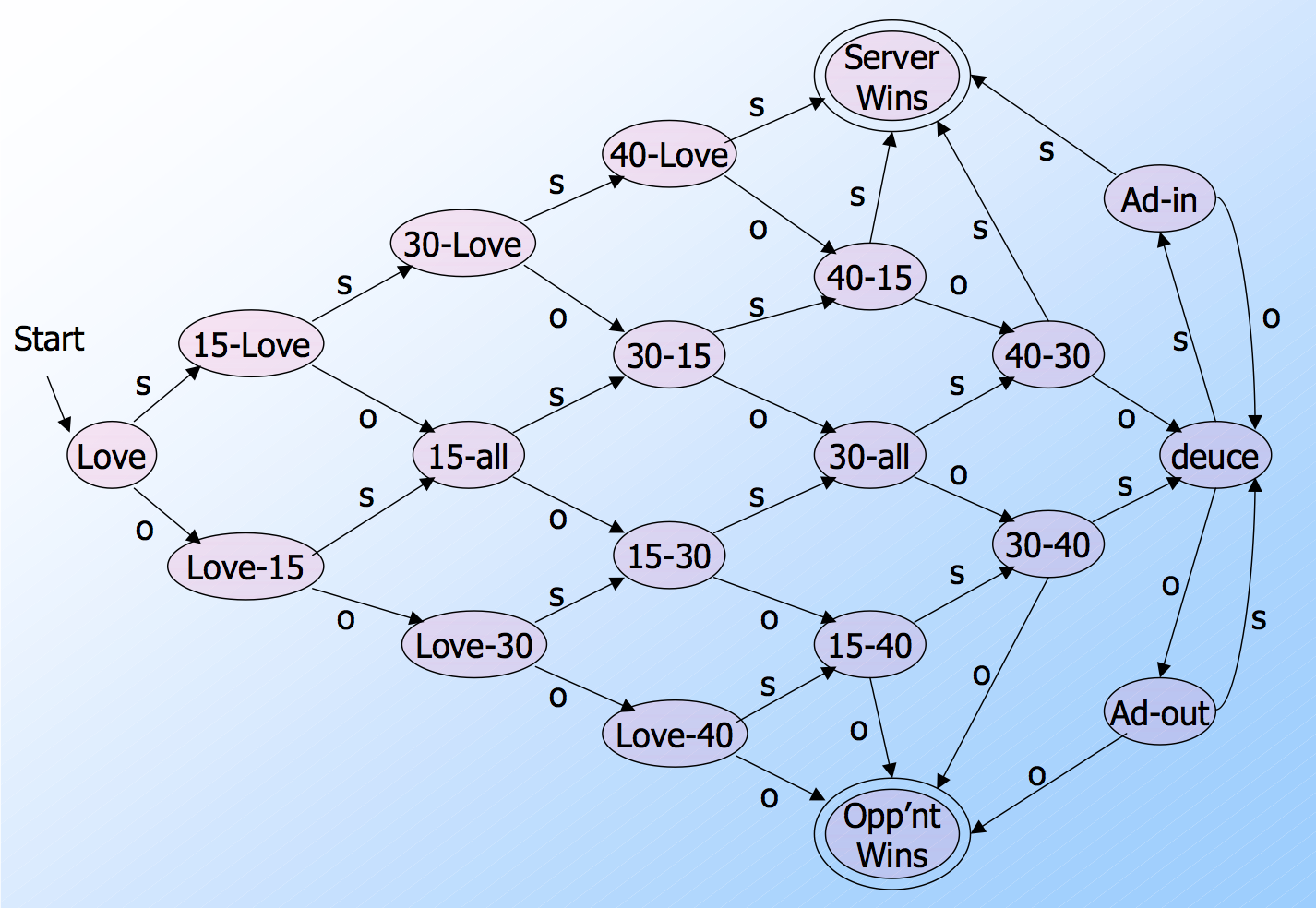
The game starts from state “Love”, and ends when either server or opponent wins, which represents end states. The automaton accepts strings which a winner is decided. If neither player can lead by 2 points, the game would transform back and forth between “deuce” and “Ad-in” or “Ad-out”. By the way, the Isner–Mahut match at the 2010 Wimbledon Championships holds the record for the longest tennis match, which lasts for 11 hours, 5 minutes, in 3 days, with the final score 70-68. I happens to watch the news at that time, and how time flies.
Language of an Automaton
- The set of strings accepted by an automaton A is the language of A. Denoted as L(A).
- Different set of final states => different languages.
- Example: As designed, L(Tennis) = strings that determine the winner.
Deterministic Finite Automata
Alphabets, Strings, Languages
- An alphabet is any finite set of symbols, e.g. {0, 1}.
- A String over an alphabet $\Sigma$ is a list, each element of which is a member of $\Sigma$, e.g. 01001, $\epsilon$ (empty string).
- A Language is a subset of $\Sigma^*$ (set of all strings) for alphabet $\Sigma$.
DFA
A formalism for defining languages, consists of
- A finite set of states, $Q$
- An input alphabet, $\Sigma$
- A transition function, $\delta$
- A start state, $q_0$
- A set of final state, $F$
Where the transition function $\delta$ takes a state $q$ and an input symbol $a$, and output the state that the DFA goes to when $q$ and $a$ received. A DFA can also be represented as graph, and transition table.
Language of DFA
- Automaton of all kinds defines languages
- $L(A)$ is the set of strings labeling paths from the start state to a final state, or formally
$$
L(A) = \{w | , \delta(q_0, w) \in F\}
$$
The transition function on string $w = xa, , a \in Q$ can be computed recursively,
$$
\delta(q_0, w) = \delta(\delta(q_0, x), a)
$$
Regular Language
A language $L$ is regular if it is the language accepted by some DFA. Unfortunately, there exists non-regular languages, for example, $L_1 = \{0^n1^n | \, n \geq 1\}$.
Nondeterministic Finite Automata
A nondeterministic finite automata has the ability to be in serval states at once, which means transitions from a state on an input symbol can be to any set of states. The NFA also start in one start state, and accept a string if any sequence of choices of transitions leads to a final state. The intuition is that the NFA always “guesses right”. Formally, an NFA is
- A finite set of states, $Q$
- An input alphabet, $\Sigma$
- An transition function, $\delta$
- A start state in $Q$, typically $q_0$
- A set of final states $F \subset Q$
Now, $\delta(q, a)$ is a set of states, contains all the states the NFA can go to, when in state $q$ and symbol $a$ received. The extended transition $\delta(q_0, xa) = \cup \delta(p, a),\, p \in \delta(q_0, x)$, with the basis $\delta(q_0, \epsilon) = \{q_0\}$.
Equivalence of NFA and DFA
It seems that NFA can represent more languages, since a NFA now can go to multiple states by one step. But it turns out surprisely that for any DFA, there is a DFA accepts the same languages. The contraverse is obvious, thus DFAs and NFAs represents the same kind of languages, regular language.
Proof Sketch: For a NFA $(Q, \Sigma, \delta_N, q_0, F)$, construct the equivalent DFA using subset construction with
- States: $2^Q$ (each state is a subset of $Q$)
- Inputs: $\Sigma$
- Start states: $\{q_0\}$
- Final states = all those (subset of $Q$) contains a member of $F$
- Transition function $\delta_D(\{q_1, \ldots, q_k\}, a) = \cup \delta_N(q_i, a), \, i = 1, \ldots, k$.
Then the NFA and DFA accepts the same language. It can be proved by induction on $|w|$ that $\delta_N(q_0, w) = \delta_D(q_0, w)$, thus the NFA and DFA accepts the same strings.
NFA with $\epsilon$-Transitions
We can even allow state-to-state transition on $\epsilon$ input, these transitions are done spontaneously, without looking at the input string. Again, the extension only accepts regular language. It can be proved that for any $\epsilon$-NFA, there is a NFA which accepts the same language. The intuition is that we can combine the $\epsilon$-transitions with the next transition on real input. And the prove is also completed with induction.
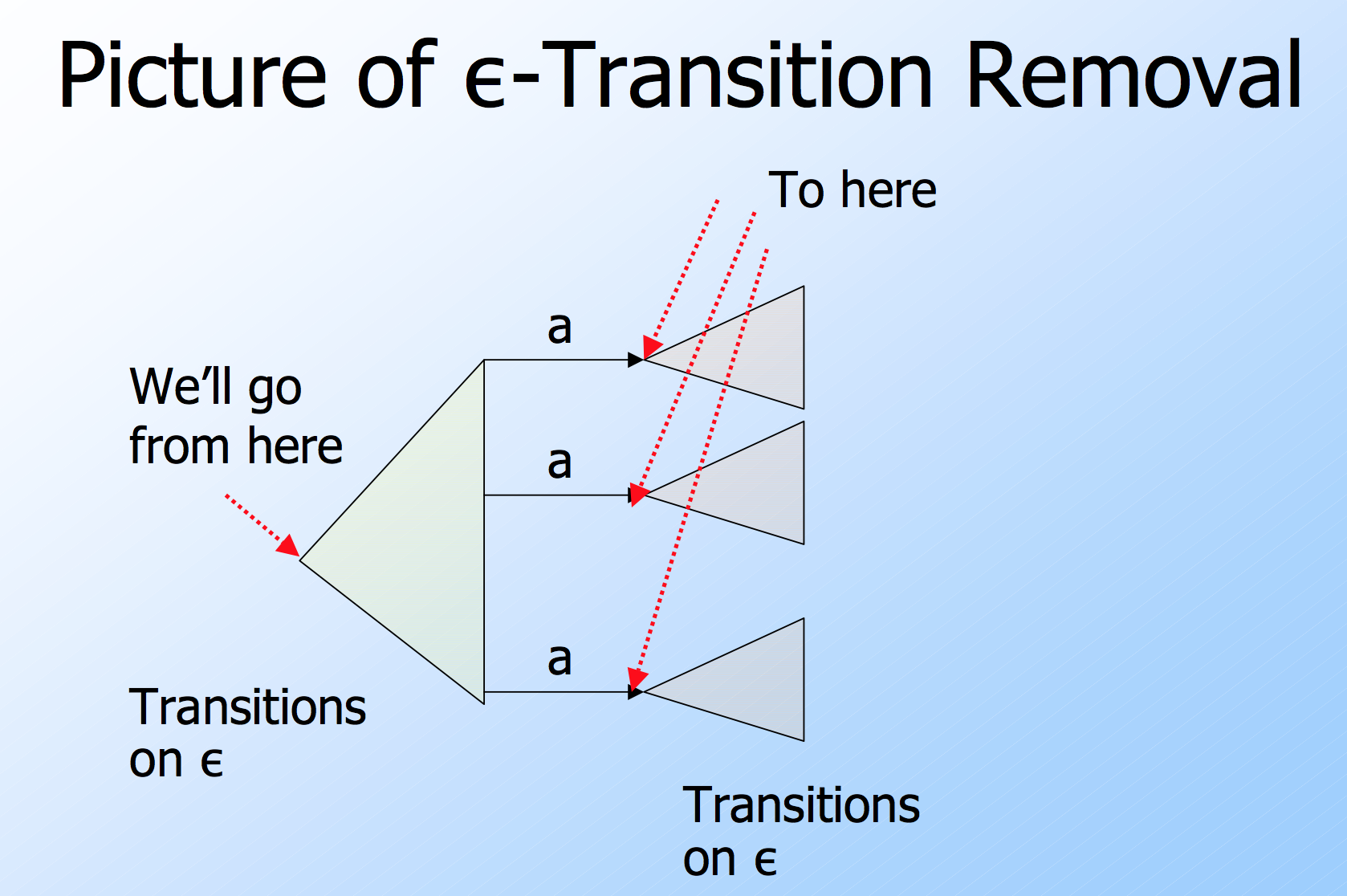
Remark
- Not so obviously, the DFA, NFA, $\epsilon$-NFA accepts exactly the same class of languages: the regular language, although the last two seem to be more powerful. It seems that regular languages is a boundary for finite automatas, which has no memory to remember previous states and symbols, and only finite states available.
- The NFA types are easier design, and may have exponential fewer states than a equivalent DFA (see subset construction).
- Only a DFA can be implemented until now.